Sunny thoughts

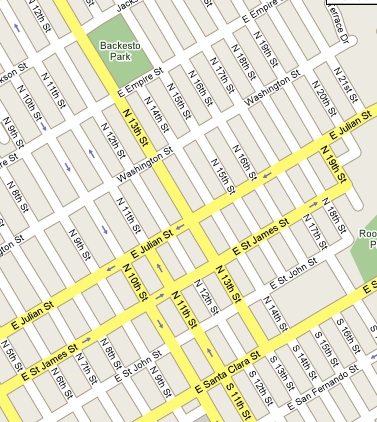
We signed up for a 3kW Photo Voltaic (PV) array last week. The sales guy took out a compass and decided that the front roof was the best place to install the array. We're looking for ward to our new PV array, but I got to thinking: is the front roof the best place to site the cells? The recommended azimuth is due south. The downtown San Jose street grid is twisted about 35 degrees from true north. The front of our house faces down and to the left, on the map so our panels would face about 55 degrees from south - around 3pm on a sundial. Our roof pitch is only "5 and 12" (about 66 degrees from the horizon). The usual advice is to shoot for an elevation equal to 90 - L +23 to give peak output in the summer. L is about 37 for San Jose, so our summer peak elevation would be 76 degrees. If you want your panels to peak at some other time of the year, you would point the elevation even lower (as far as 90-L-23 for a winter peak).
Could I improve the array output by tilting the panels? Yes, certainly. My back-of-the-envelope calculation said that I would lose 30% of my output by laying them flat on the front roof. That takes my 3kW array and makes it 2kW. Bummer. If I constrain myself to keeping one edge anchored to the roof, which edge should I pivot and how much should I tilt it? The simple math keeps the low edge on the roof and pivots the cell down about 6 degrees (or 33 degrees or even 50 degrees). This would change the elevation but would still leave the array pointing at a 3 pm sun.
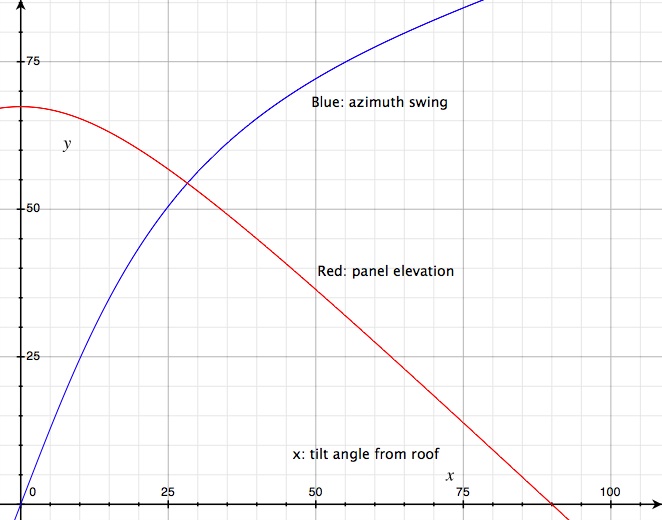
What if I pivot up from the side of the cell? Well, the math gets a little more complicated, but the basic idea is that I can swing the azimuth towards due south and bring the elevation down at the same time - a two-fer! After scratching my head for longer than I care to admit, I remembered some long-forgotten math about rotational matrices... A little algebra and I came up with the equations describing the cell angle.	Here's the mac Grapher file, for anyone who wants to play with it: SolarAnglesOne.gcx If you decide to use it, make sure to use the correct "a" for you roof. The graph I'm showing is for "5 and 12" roof pitch.
[some nice 3-D animations would be nice, here. Maybe I can convince someone who is also checking my work to illustrate it (hint, hint).]	The angles are relative to the house orientation - you can use this no matter what direction your house faces.
Result: If I prop up the side of each panel to about 22 degrees, it swing mys panels 45 degrees south, and brings my elevation angle down to about 60 degrees. I could also put the panels on the south-east side of the roof. Then, a panel tilt of only 13 degrees would point me due south and I would get a little better elevation of 64 degrees. 22 degrees requires 13.5" over the 36" short dimension of the panels. 13 degrees only takes 8" of boost.	keywords: sun angle, insolation, solar cell installation

Now I just need to convince the installer to prop up one edge of each panel by 13.5" (22 degrees over a 36" radius), or something.

For those who want the gory details:

In 3 dimensions, we start with a vector that represents the direction the panel is pointing when it's laying flat on the ground. I've picked y as my "up" axis - it really doesn't matter as long as you don't forget which is which.

p={0,1,0}

Now I use 2 rotational matrices: R for the roof and T for the side-tilt that I'm adding. (I'll use bold to indicate a matrix). The result of applying the 2 rotations is the q vector.

q = R * T * p

In constructing R, I chose to rotate around the z axis:
The roof tilt angle is "r"

	cos(r)	-sin(r)	0
R=	sin(r)	cos(r)	0
	0	0	1

I used x as the T pivot axis:
I "t" is the side-tilt angle.

	1	0	0
T=	0	cos(t)	-sin(t)
	0	sin(t)	cos(t)

Now, to tighten this up into a single matrix, I'll multiply R and T to get a new matrix: B.
The new equation will look like this:

B = R * T
and
q = B * p

and B is:

	cos(r)	-sin(r)*cos(t)	sin(r)*sin(t)
B=	sin(r)	cos(r)*cos(t)	-cos(r)*sin(t)
	0	sin(t)	cos(t)

multiply by the flat panel vector (p)
and I get the equations for x, y, and z or the result vector (q)

x=-sin(r)*cos(t)
y=cos(r)*cos(t)
z=sin(t)

But I want the angles in azimuth and elevation, so let me use the inverse tangent. atan2() takes x and y separately, instead of just the quotient.

azimuth = atan2(z,x)
elevation = atan2(y, sqrt(x^2+z^2))

or

azimuth = atan2( sin(t), -sin(r)*cos(t))
elevation = atan2(cos(r)*cos(t),sqrt(sin^2(r)*cos^2(t)+sin^2(t)))

Now, I discover that "r" has a special meaning in Grapher (of course)
so I used "a" instead of "r". I want the angles to plot as y values, so I'll write two equations for y (that's how you get 2 lines in Grapher).

And, I really want to graph this stuff as a function of the side-tilt,
so I replaced "t" with "x". Don't confuse this x with the original x axis.

azimuth:
y = atan2(sin(x), -sin(a)*cos(x))

elevation:
y = atan2(cos(a)*cos(x),sqrt(sin^2(a)*cos^2(x)+sin^2(x)))

Later,
Bob
home